Overview

In this project, I was able to understand how to manipulate a set of points to create particular continuous curves know as Bezier Curves, and how to implement these curves into surfaces using de Casteljau's algorithm. I also created a mesh editor with functions that smoothen meshes by manipulating normal vectors, make use the Half-edge data structure to flip and split edges of meshes, as well as use loop subdivision in order to upsample meshes and create smoother mesh objects. Through this project I also learned about the meticulousness of pointers in general, and the necessity to keep track of all variables in order to yield successful code.

Section I: Bezier Curves and Surfaces

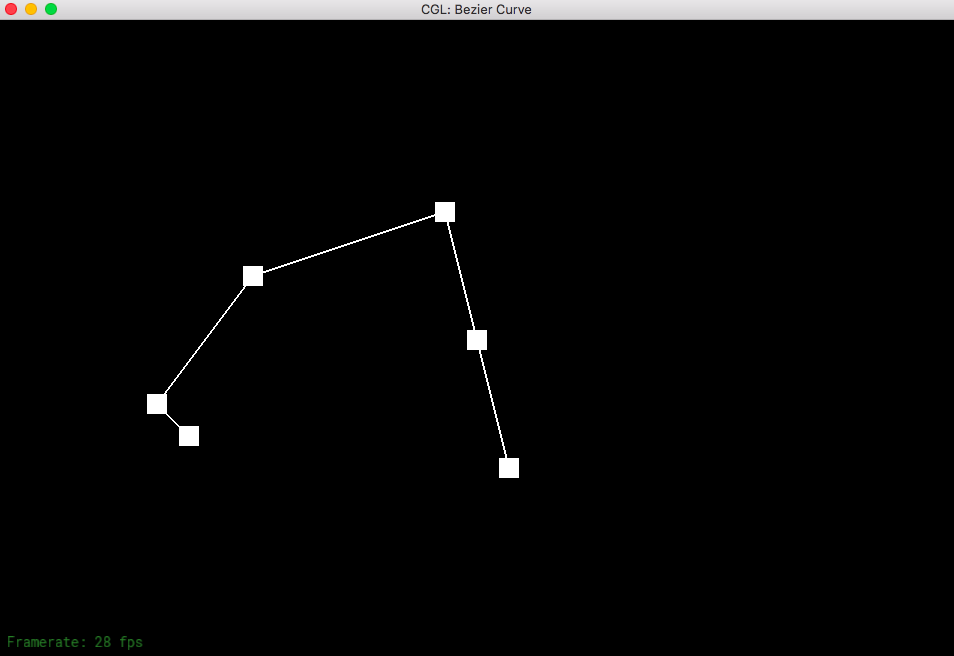
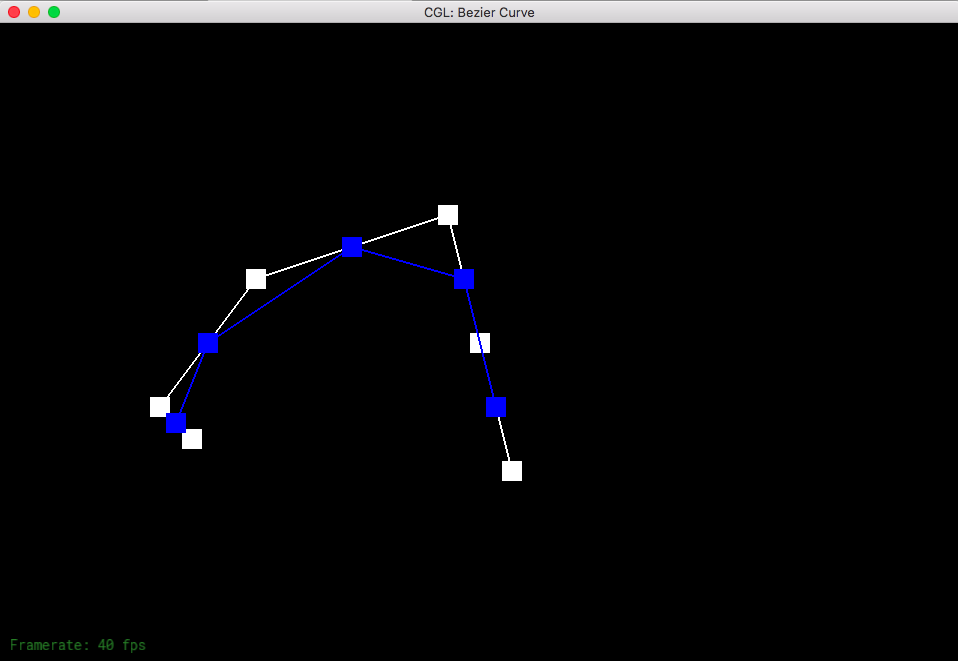
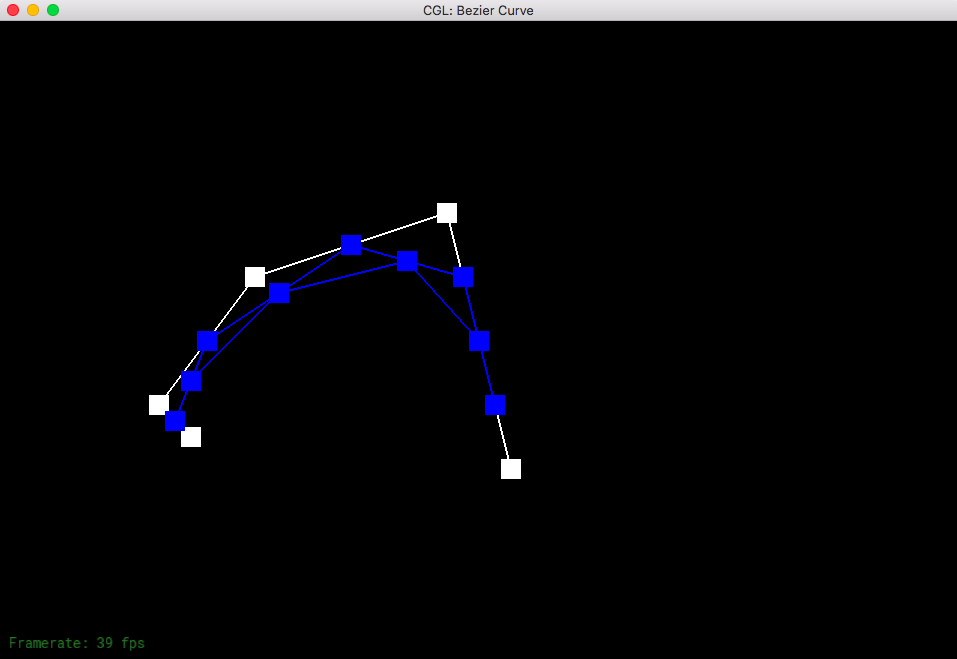
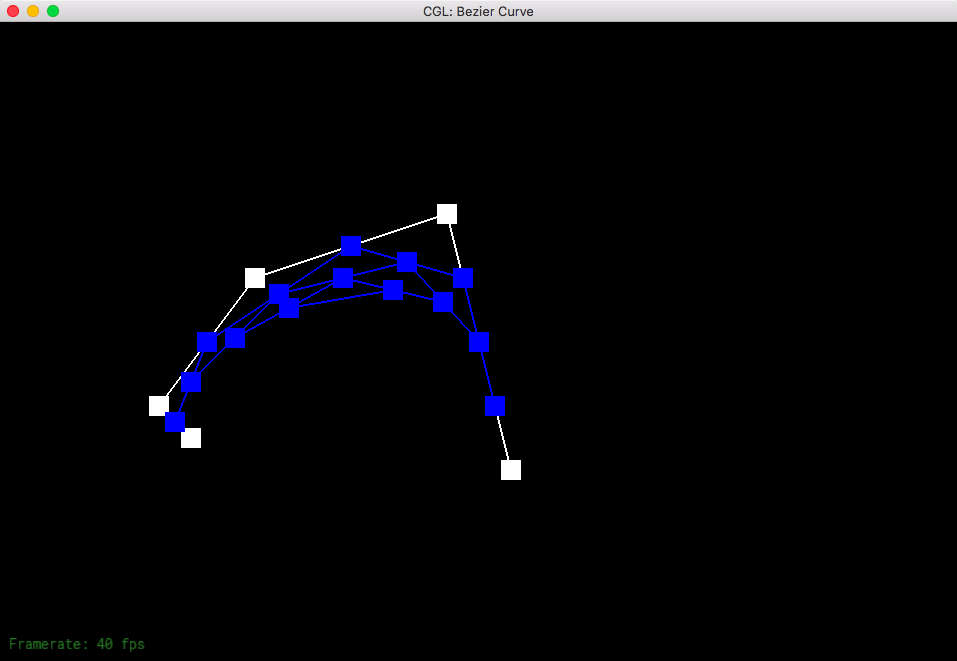
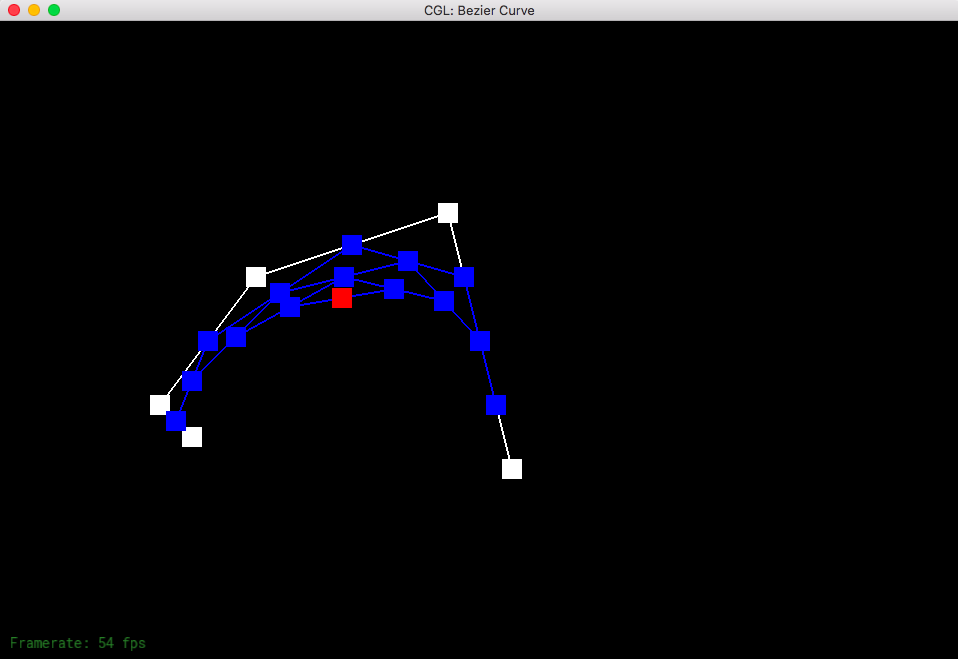
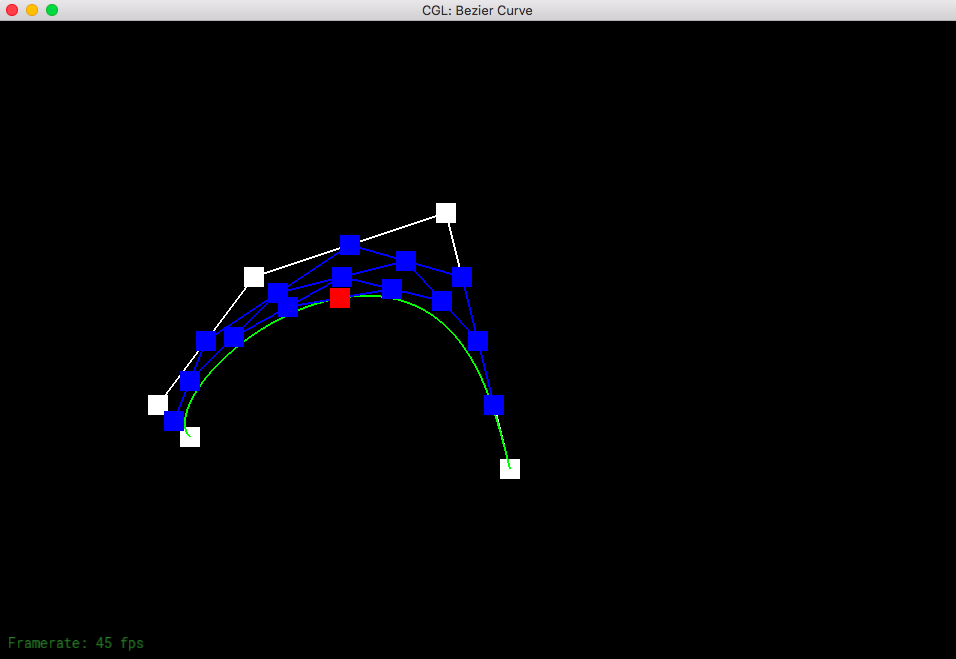
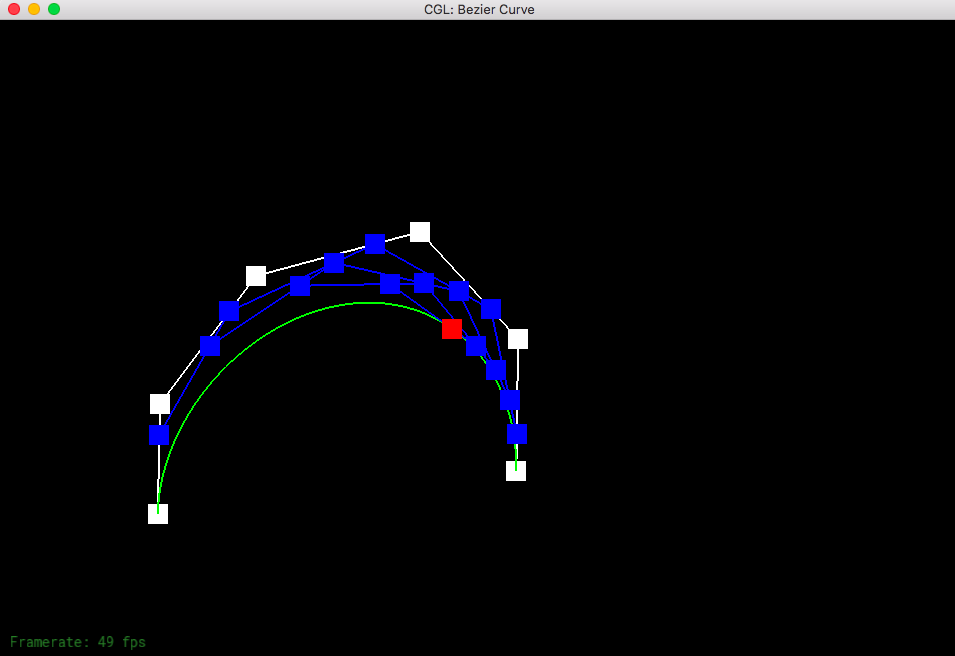
Part 1: Bezier curves with 1D de Casteljau subdivision

De Casteljau's algorithm is a recursive method that allows us to calculate a Bezier curve from a set of points. The process for doing so is to connect the points to create edges; we then evaluate each edge at a parameter in between 0 and 1.0, which represents a fraction of the distance from one point to the other point. We connect these points to get a connection of edges that is one less than the number of edges previously. The recursive linear interpolation steps finish with one point, allowing us to come up with a tangent point which we draw our curve to.

Part 2: Bezier surfaces with separable 1D de Casteljau subdivision

De Casteljau's algorithm extends to surfaces because I can apply what I did for the 1 dimensional curve, and just add another dimension to create a 2 dimensional surface. Applying multiple Bezier curves together would create a Bezier surface. I used a method called "Separable 1D de Casteljau", which does Casteljau in one dimension (the u dimension) first, and then uses those values to compute Casteljau in the second dimension (the v dimension).

Section II: Sampling

Part 3: Average normals for half-edge meshes

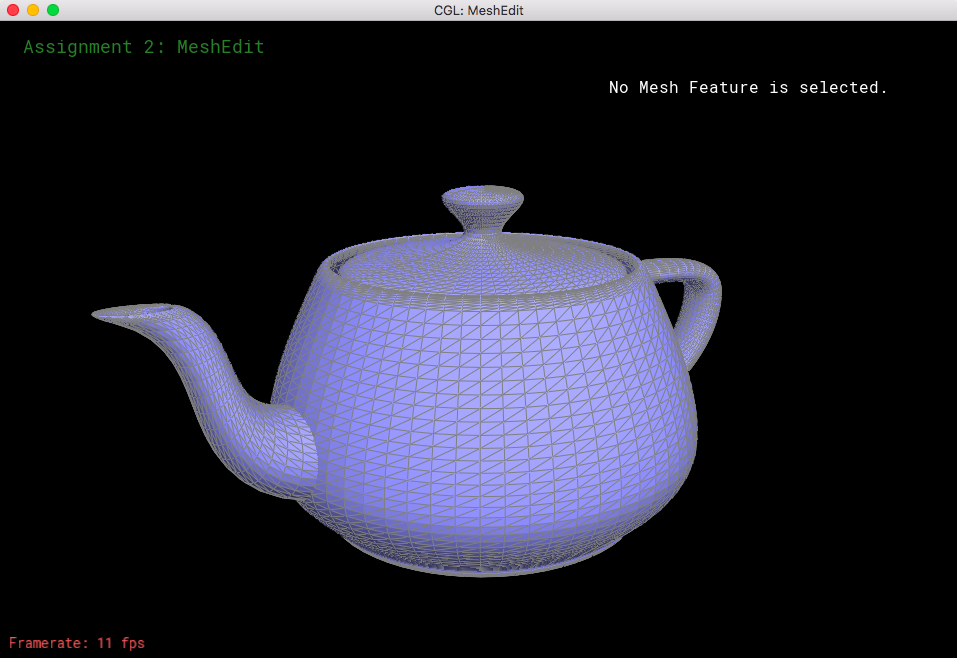
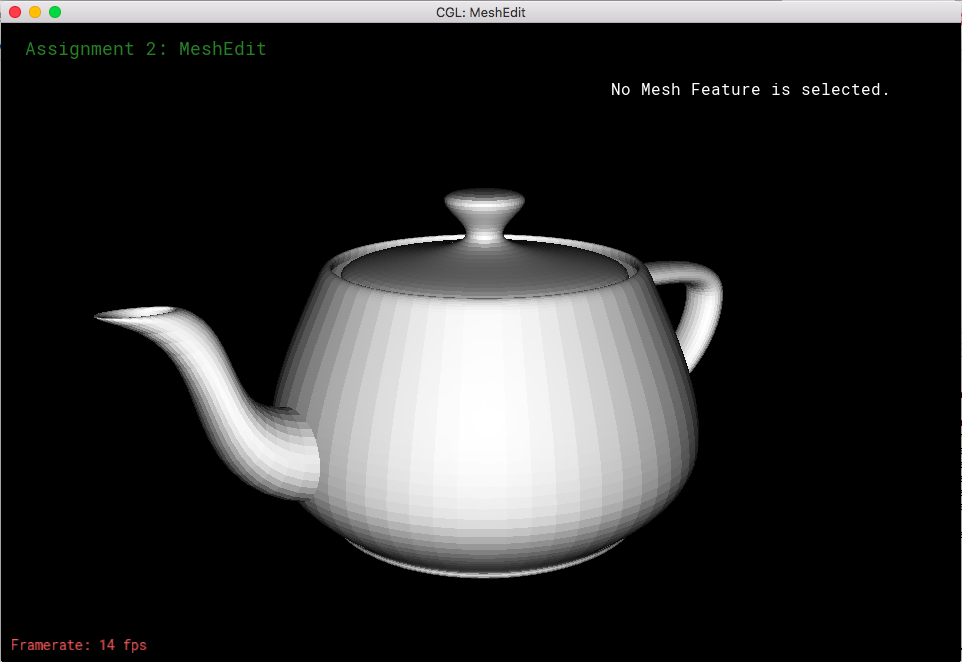
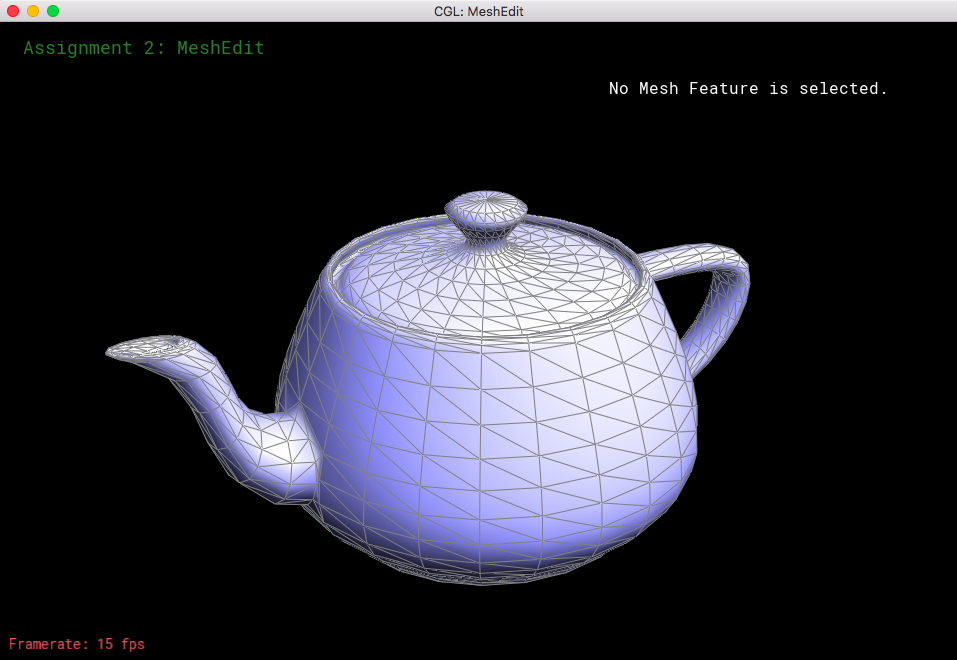
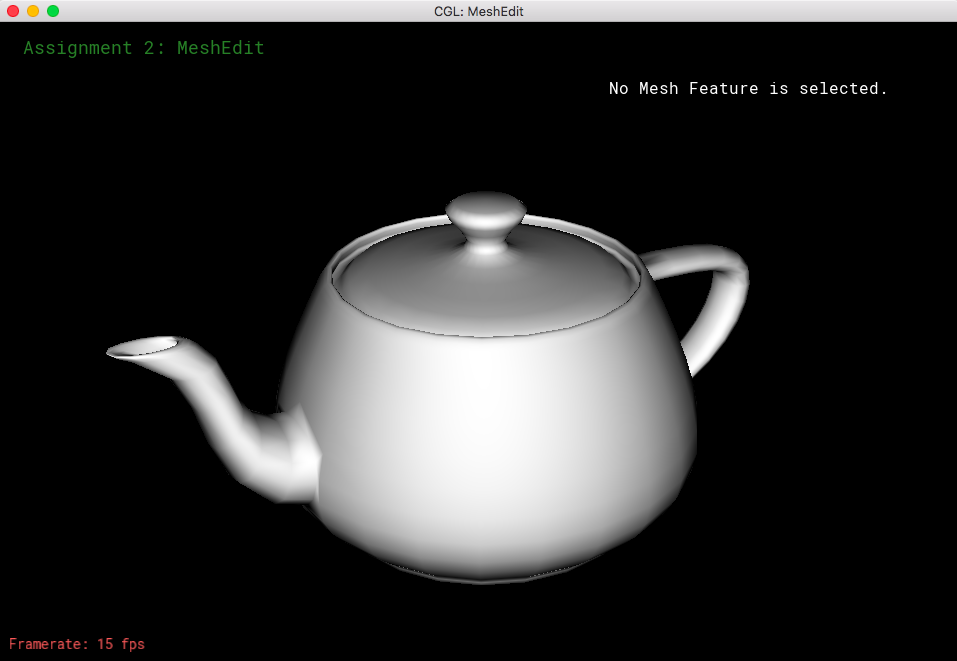
In this section I implemented the normal function, which iterates through all of the triangles that surround a certain vertex. With each triangle, I get the two edges that are connected to the single vertex and calculate the normal of these two edges (treated as vectors). I add all of these normals to get a final vector, which is a re-normalized unit vector. This allows the meshes to appear more continuous and smoother.

Part 4: Half-edge flip

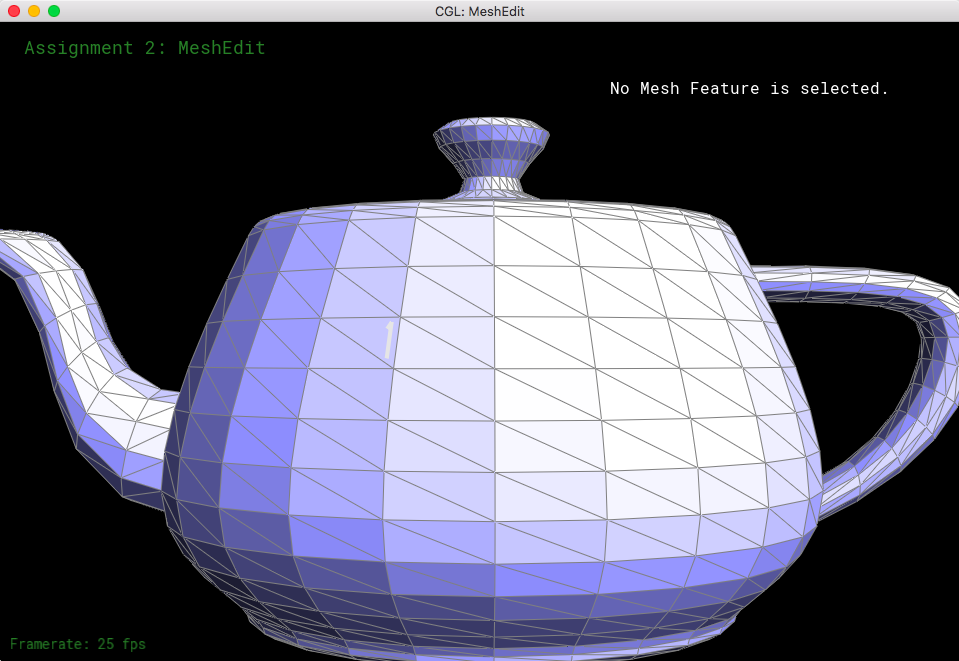
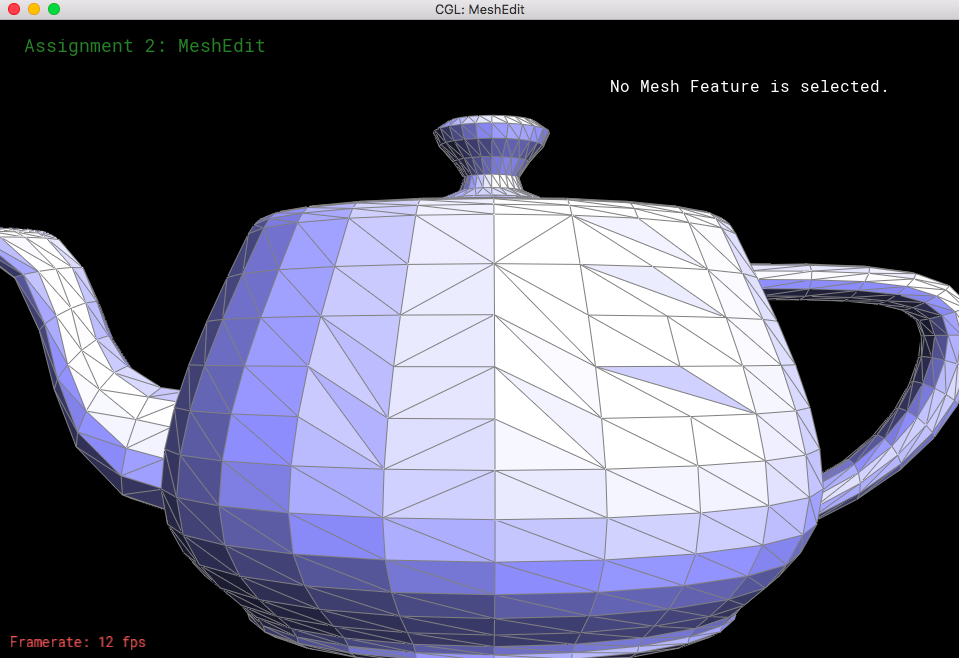
In this section, I implemented a method that, given an edge that is in between two triangles, flip orientations such that the edge would change to be spanning across the other two corners of the two triangles.

My method for flipping half-edges was to keep track of all of the half-edges inside both triangles, and having the faces, edges, and vertices point to one of the two middle half-edges. After that, I used the setNeighbors function to update the other half-edges to make two different triangles. Debugging was a nightmare. I didn't really have much to look at besides my code, and halfway through, I realized that I mixed up the face parameter with the edges parameter in setNeighbors, which was dissapointing. Also, I didn't know that I also had to update the half-edges of the faces, vertices and the edges, until the last moment, so I was trying to figure out what was going wrong when some of the edges disappeared from the mesh. Overall, I was satisfied that I was able to make a fully functioning flipEdge function.

Part 5: Half-edge split

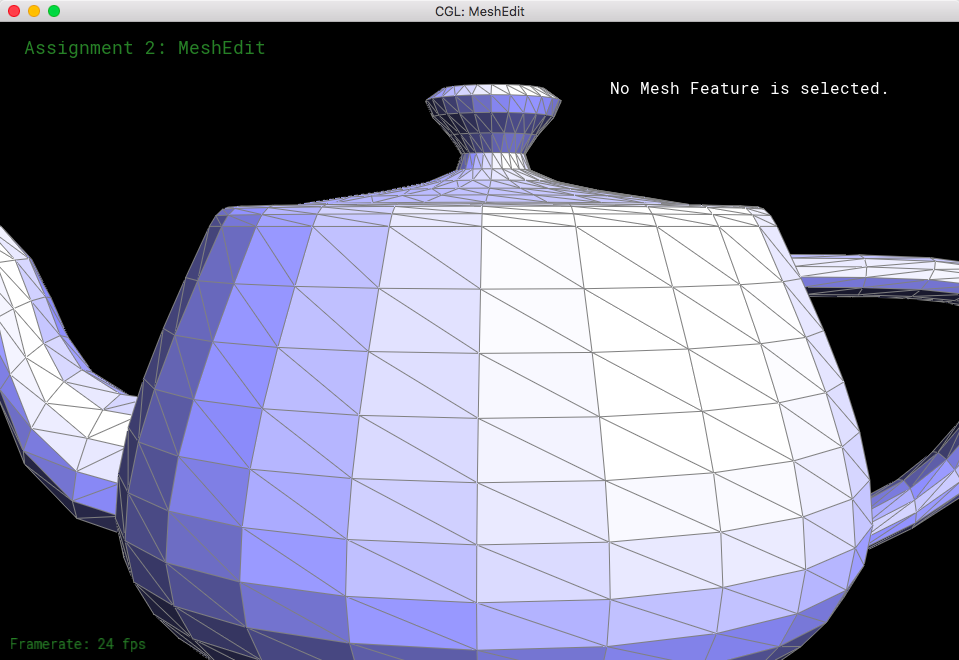
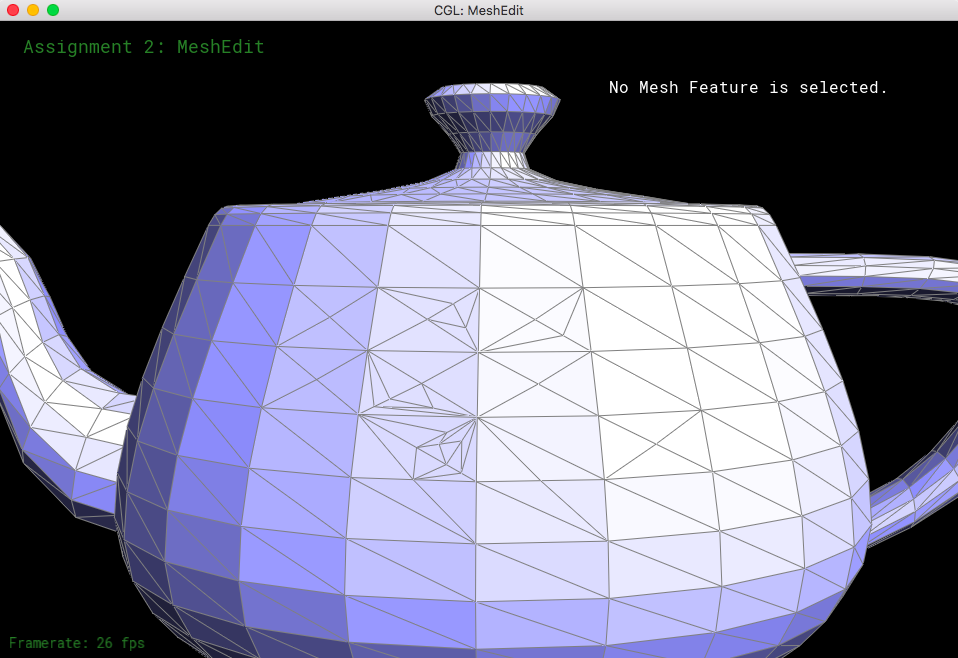
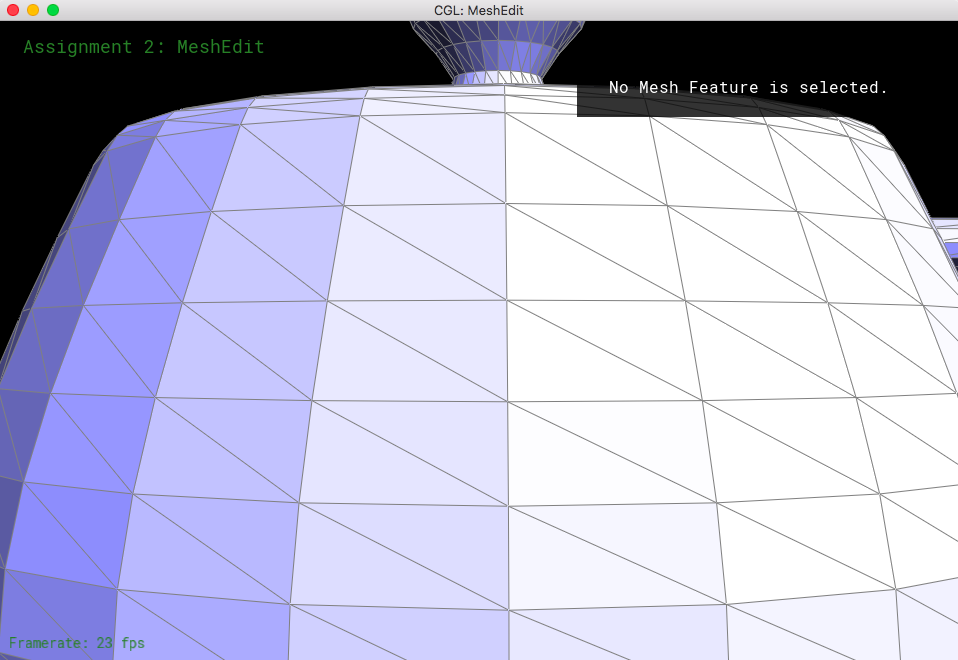
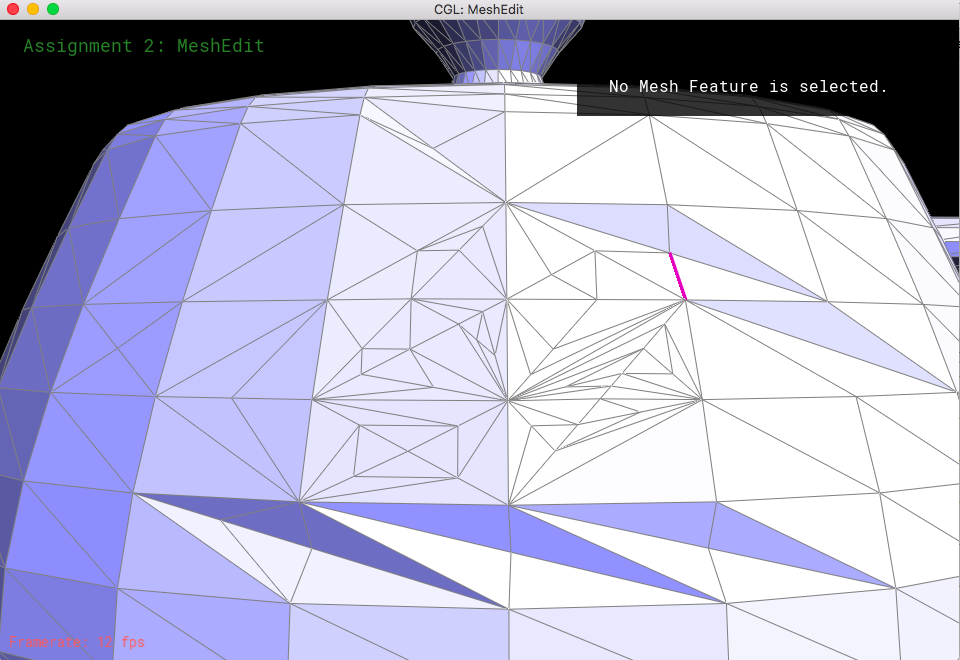
Half-edge splitting is a method that essentially creates four triangles from two adjacent triangles by inserting a new vertex in the midpoint of the shared edge, and connecting the opposite vertices of the two triangles through that vertex. Splitting half-edges is a challenge when needing to keep track of pointers and variables.

I started by keeping track of all of the possible elements (half-edges, vertices, edges, and faces) of the two triangles. Then, I allocated memory for 1 vertex, 3 edges, 2 faces, and 6 half-edges. The new vertex was just the middle distance between the two endpoints of edge e0 (which was the given parameter). I reassigned pointers for many of the elements, so that it would portray splitting both triangles right down the halfway point, where there would be 4 half-edge cycles rather than 2 half-edge cycles. This also meant that I had to change the half-edges that the vertices, edges, and faces held, as well as change the twins of most of the half-edges. The biggest challenge I faced was having to figure out the cause of my segmentation fault - it was because I did not update all of my pointers! I ended up realizing this after running through my messy code, and afterwards I decided to just rewrite my code in the format of this document:

http://15462.courses.cs.cmu.edu/fall2015content/misc/HalfedgeEdgeOpImplementationGuide.pdf

After starting my code from scratch, I was able to implement this function successfully.

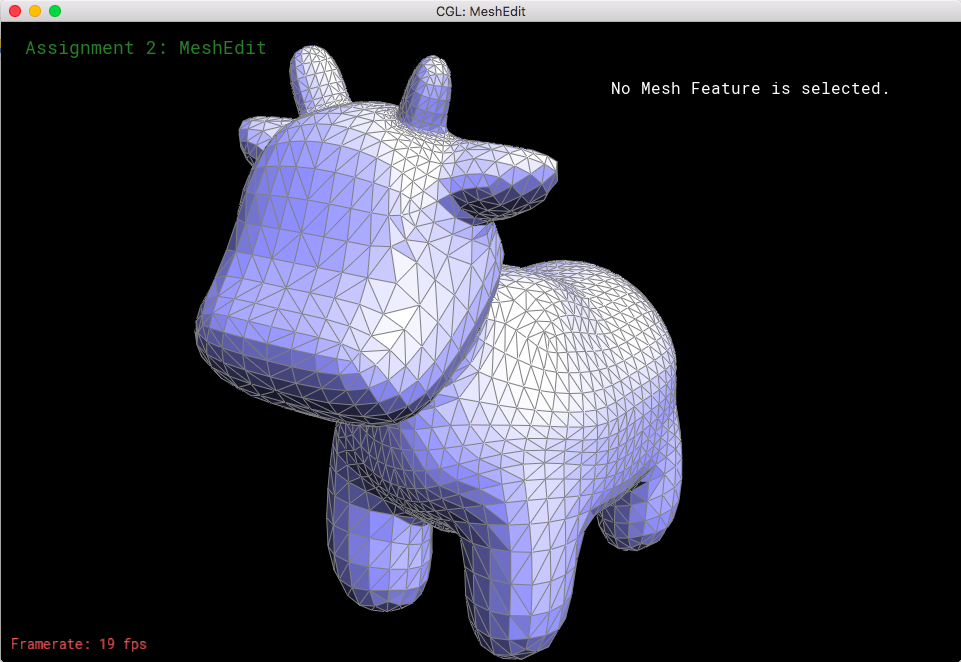
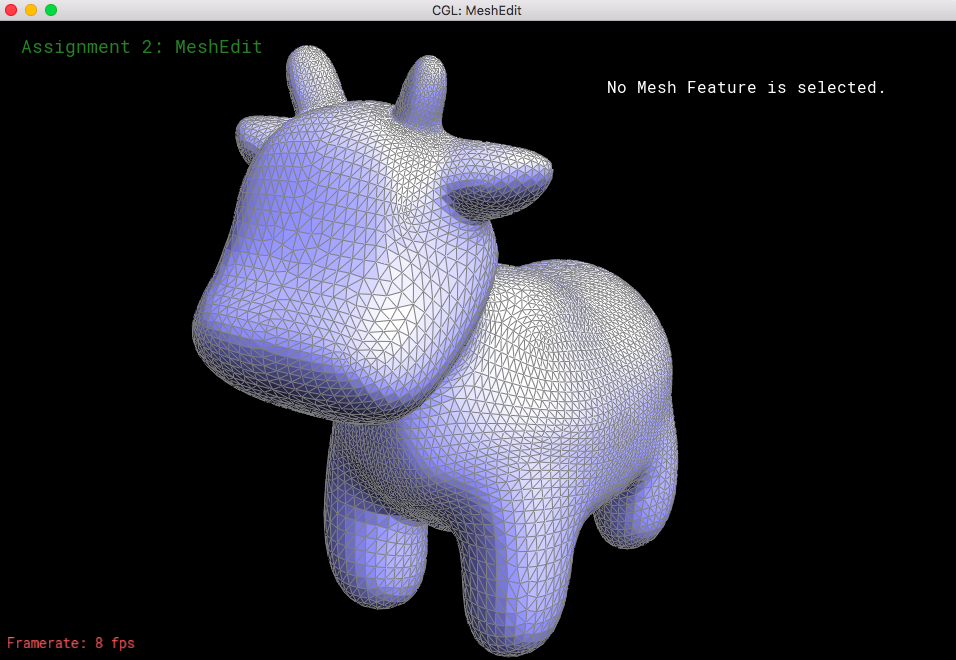
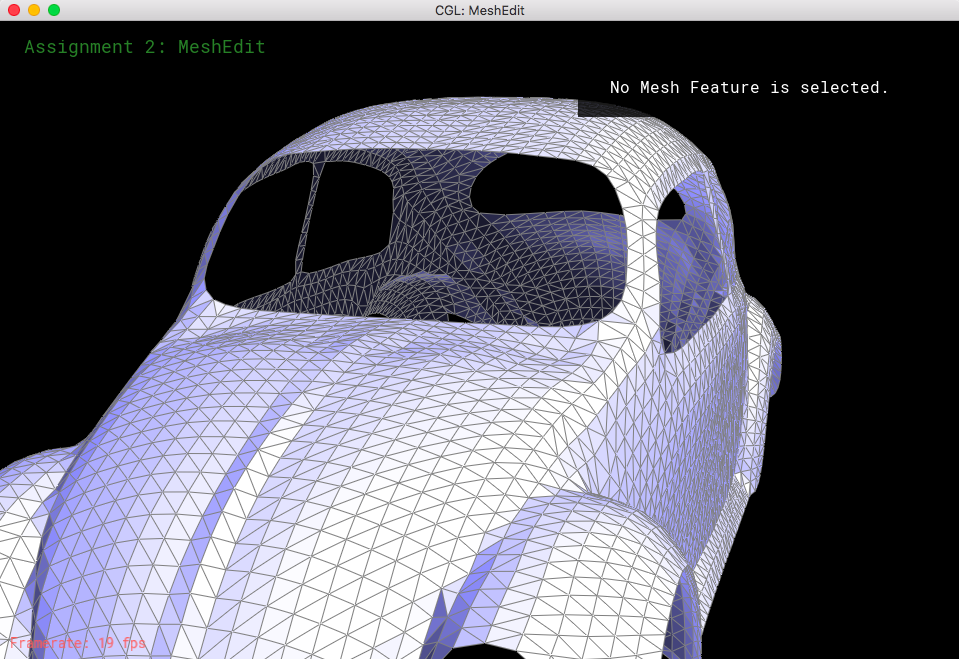
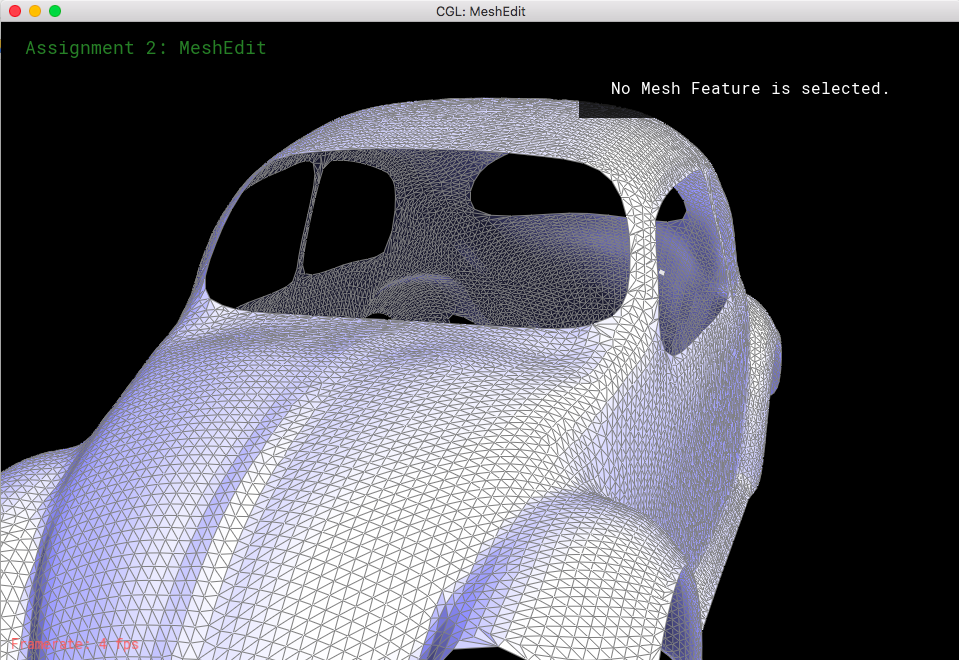
Part 6: Loop subdivision for mesh upsampling

The method behind mesh upsampling was to implement loop subdivision, which consisted of splitting every triangle into four smaller triangles, as well as adjust the coordinates for each vertex. I utilized the previous methods to perform these operations, as well as the loop subdivision algorithm to calculate the new position of all the vertices. This evidently would cause the mesh to have smaller, updated triangles that would help smoothen the overall shape of the mesh.

The way I implemented loop subdivision was first to iterate through all of the vertices, setting their isNew() values to false because these are "old" vertices. For each vertex, I add up the neighboring vertex locations as well as calculate weights that were necessary to update the vertex coordinates, using the formula (1 - n*u) * O + u * P, where O is the original position, P is the sum of the neighboring vertices, n is the vertex degree, and u is 3/16 in n = 3 (but 3/(8n) otherwise). I put these into newPosition rather than updating its actual position because we want to calculated all of the vertices' new coordinates in respect to the old coordinates, which requires the position of the neighboring vertices' old coordinates. After filling out all of the new coordinates, I iterate through all of the edges, setting their isNew() values to false as well. I also keep track of the "new position" which is just the center of each edge. This is required to have since we use these values to calculate the new coordinate when we split the edges. We use the formula 3/8 * (A + B) + 1/8 * (C + D) where A and B are the vertices connecting the current edge, and C and D are opposite vertices across the two faces connected to the two triangles with A and B. Then, I begin splitting every edge in the mesh. The problem with the splits, though, is that many of the triangles will be awkward shapes that will complicate further upsampling. So, after splitting every edge, we also flip any NEW edge that connects an old vertex with a new vertex. After we finish this, we just need to update all of the vertices to be their newPosition, to nicely interpolate the current mesh.

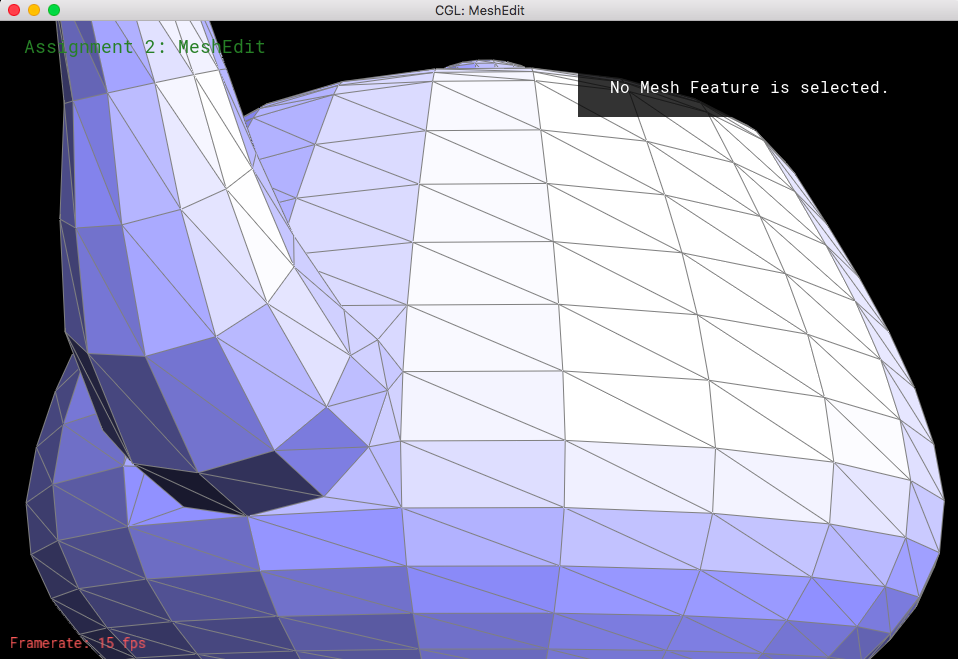
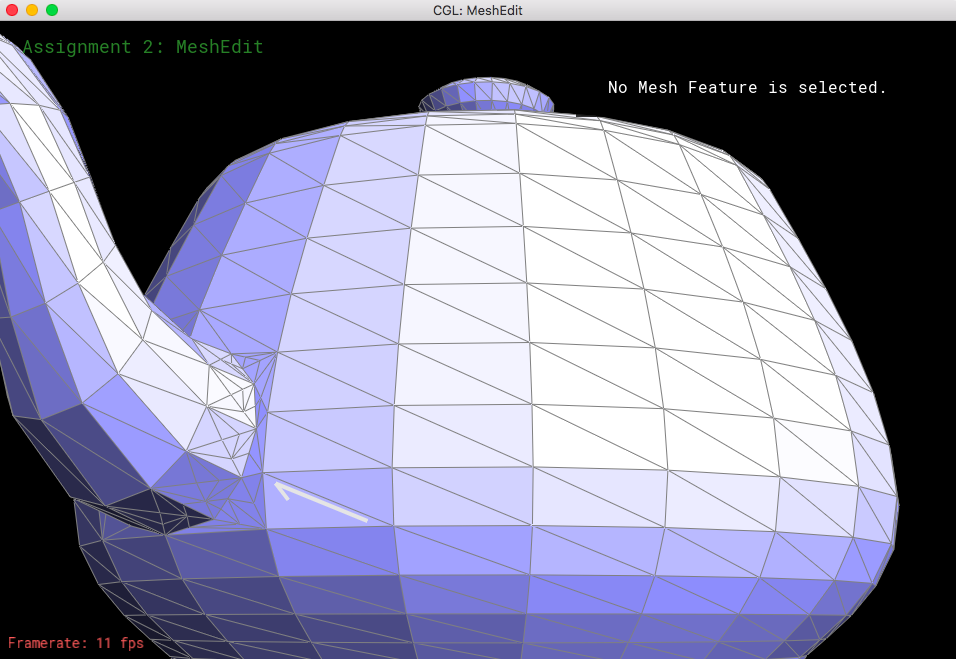
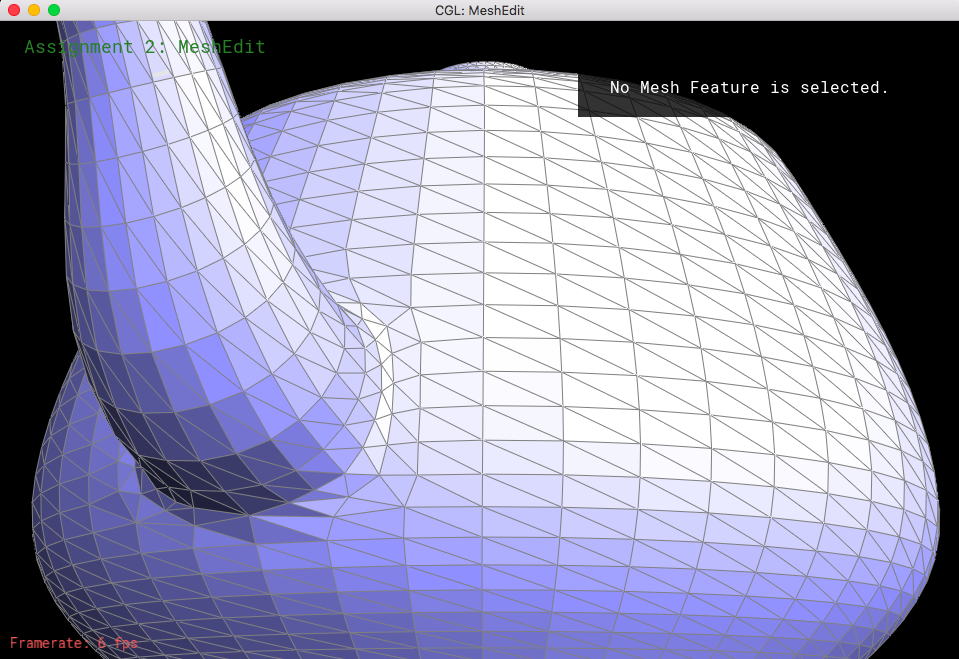
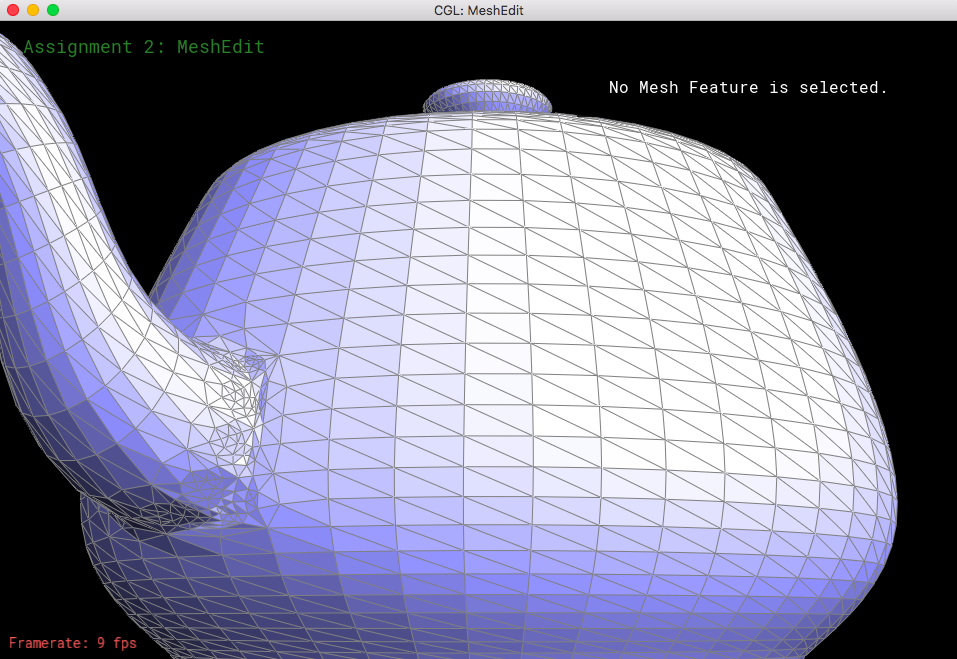
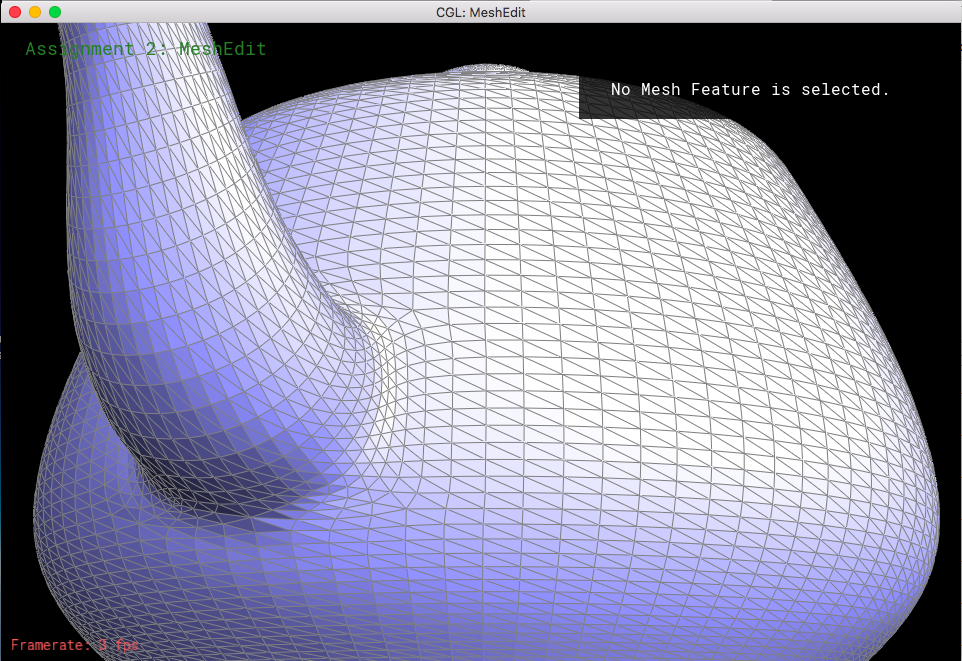
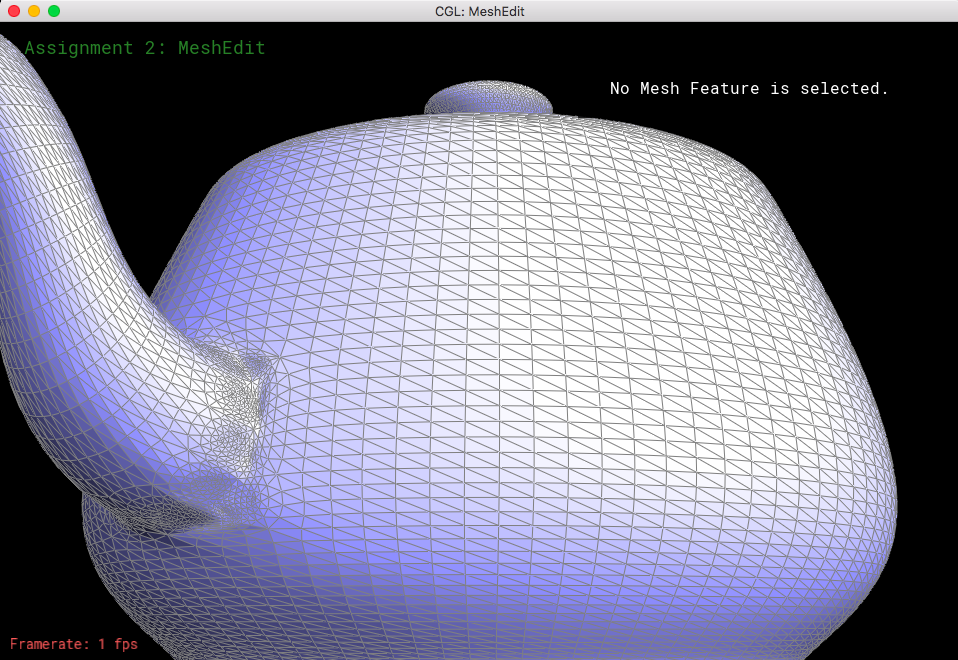
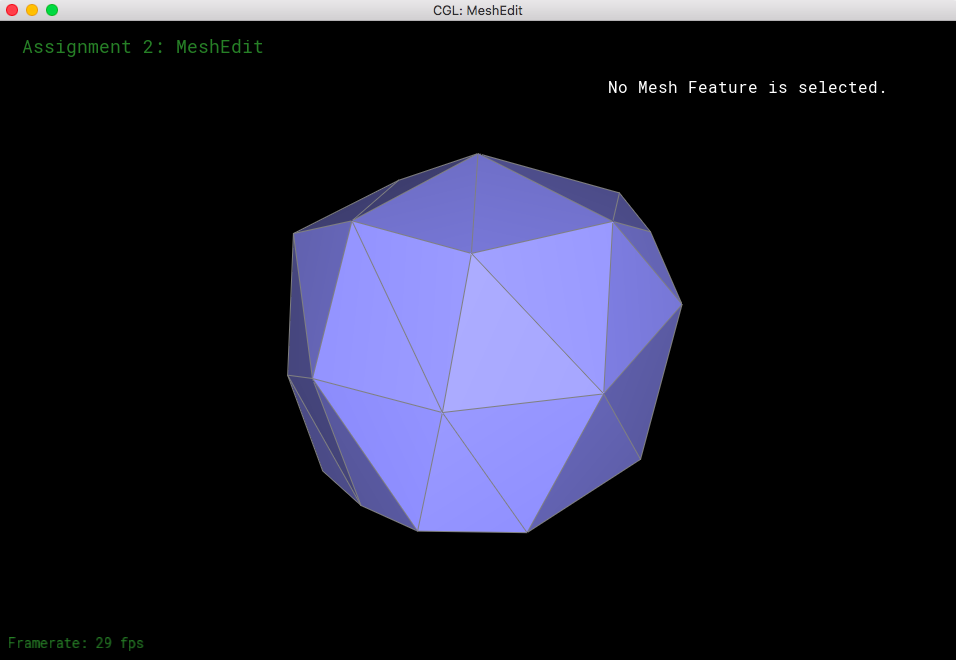
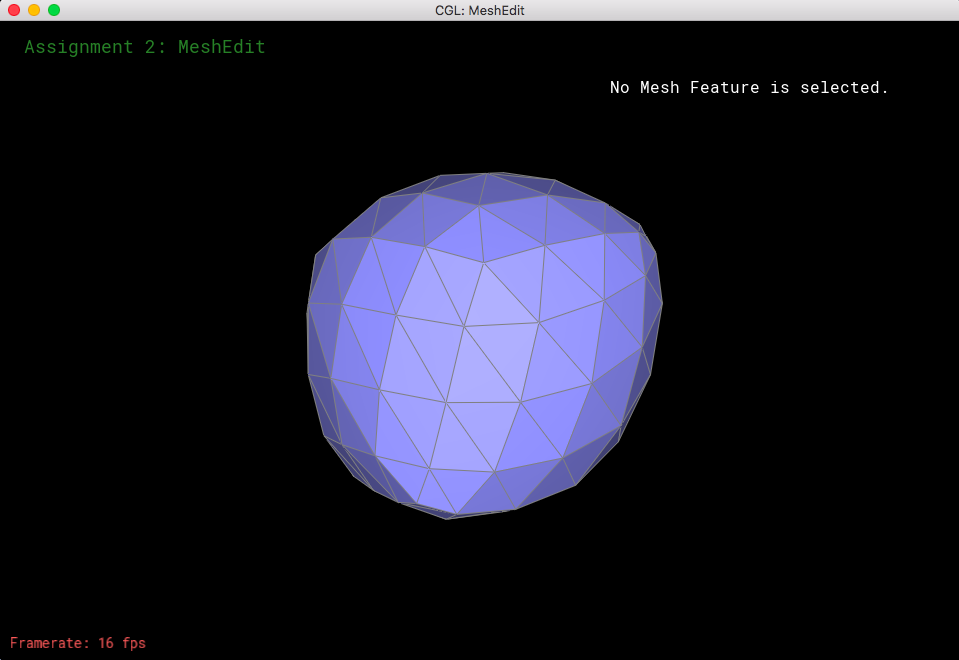
Looking at loop subdivision for some meshes, it seems that sharp edges smooth/round out more and provide a more continuous mesh.

If we were to pre-split some edges, then we can reduce the amount that gets smoothed out. This makes the sharp edges less smooth and little more defined.

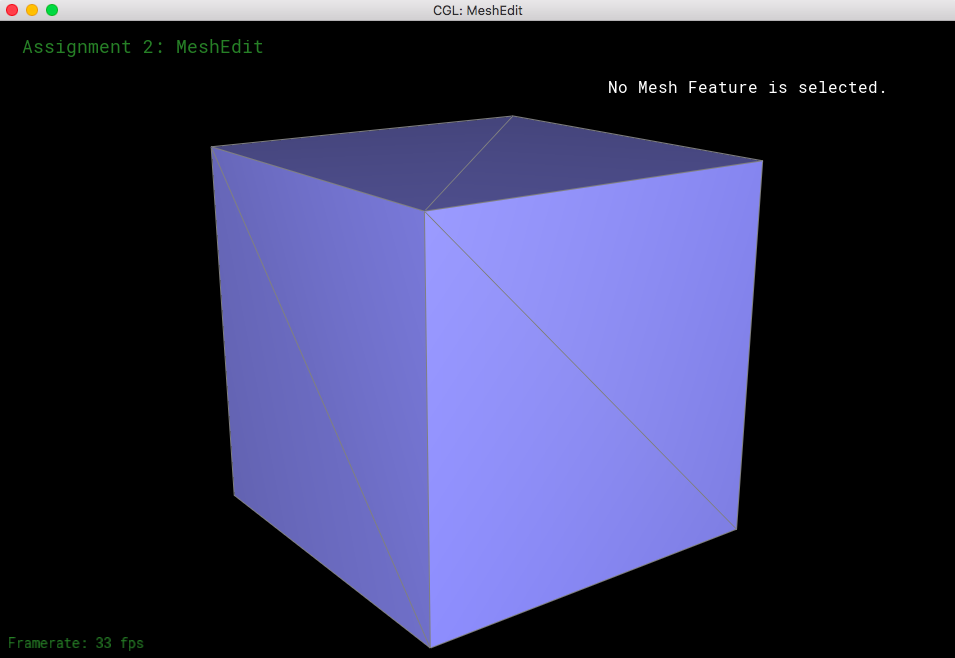
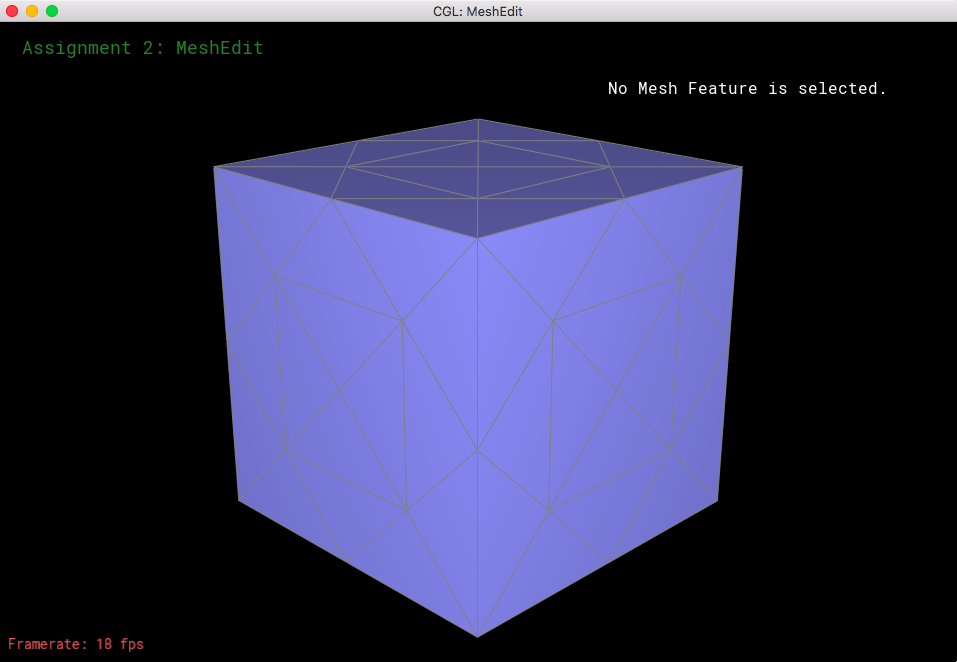
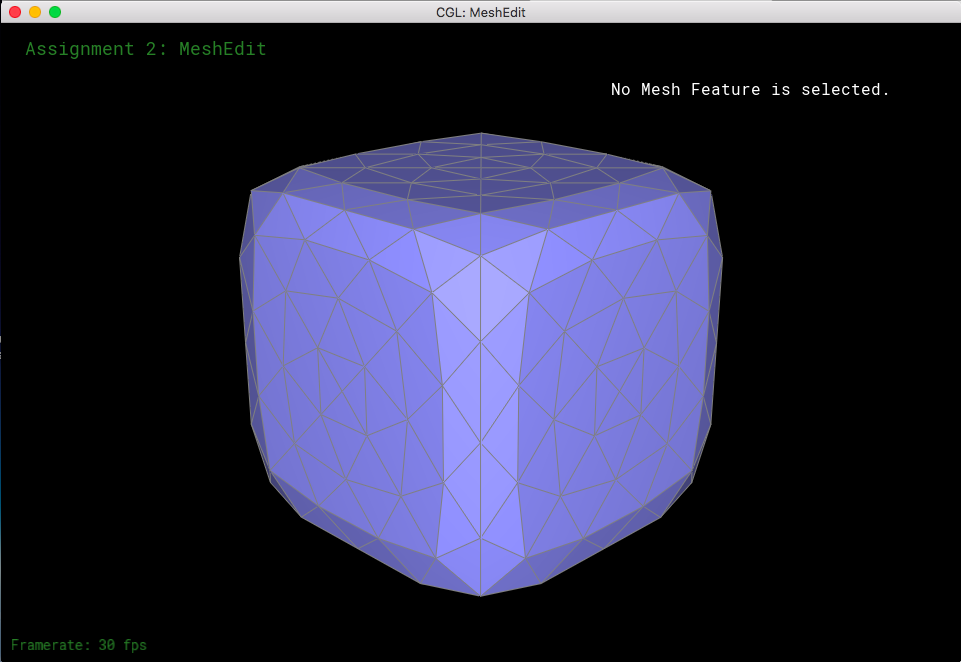
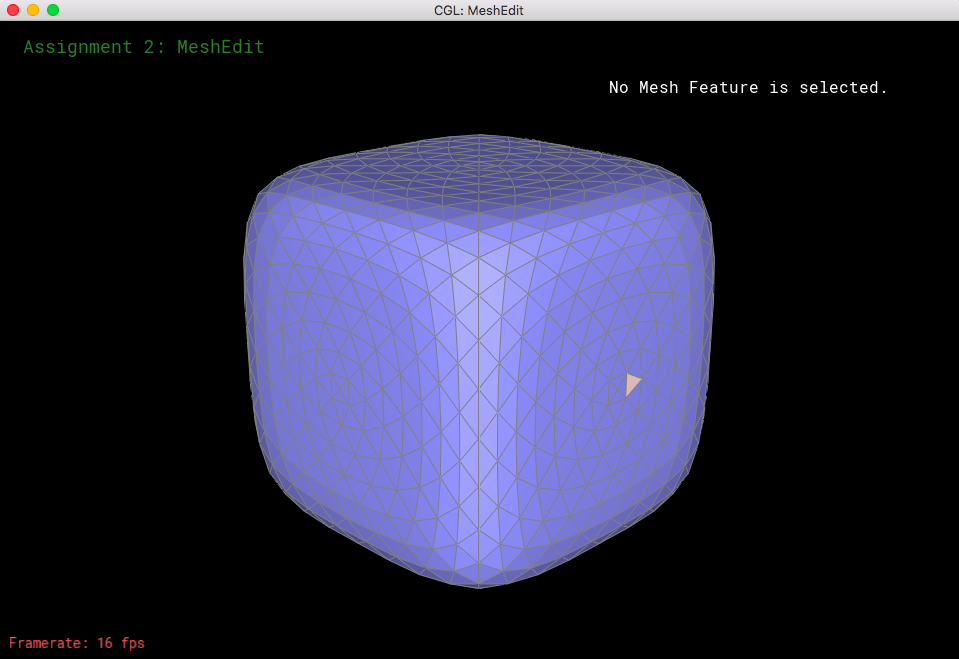
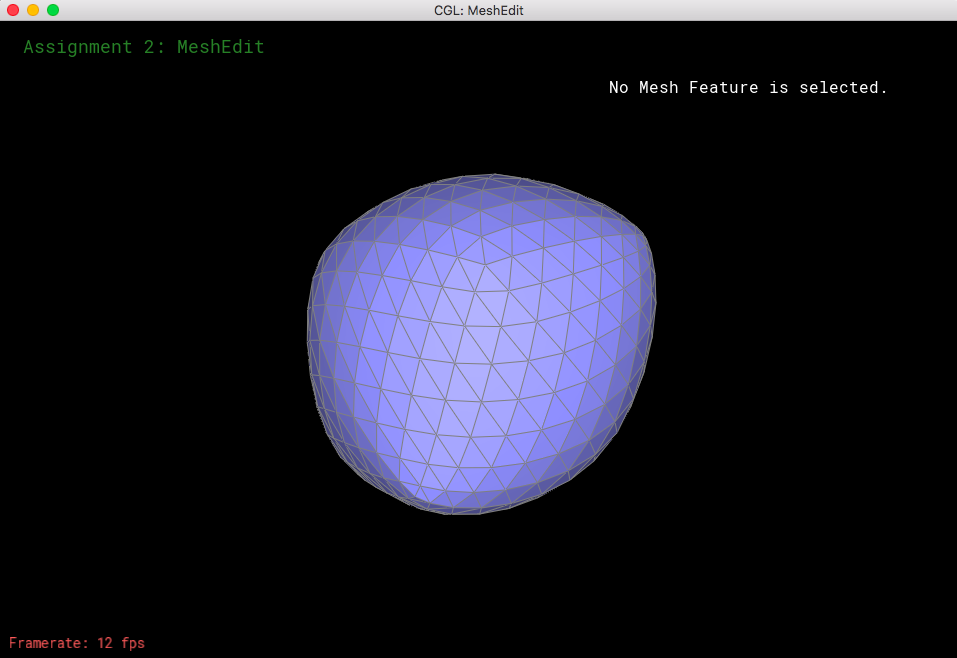
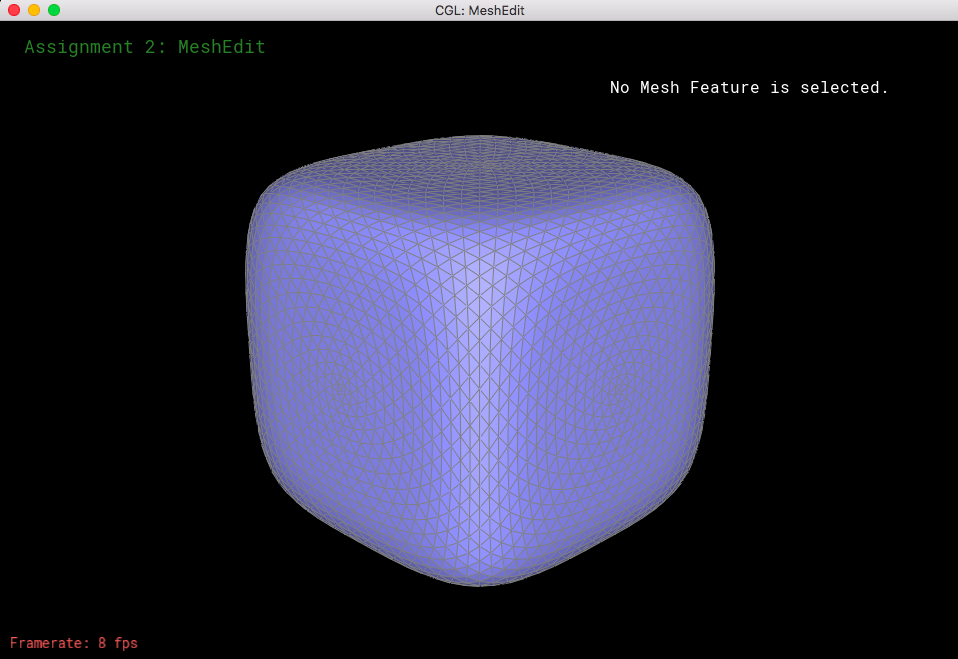
Now let's see what happens when we perform loop subdivision on the cube mesh. If we have consistent meshes and mesh splits/flips, then that would make the loop supdivisions symmetrical. The mesh was becoming asymmetric after upsampling because of the orientation of the triangles; when we take a look at the corners of the mesh, each of them have different amounts of edges coming towards them (some vertices have a degree of 3, some have a degree of 4, etc). So, when we do loop subdivision, the new coordinates would be different because we have a different n value for every corner (n represents the degree of the specific vertex, which is essential for calculating the new coordinates of each vertex). What I did to "fix" this was to split each of the edges on the face, as well as flip certain edges so that every mesh became symmetrical and every corner had the same amount of edges coming out of it.